Espen Haug
Will the exam provide N(d1) and N(d2) or do we need to calculate them? | Forum | Bionic Turtle
How to interpret N(d1) and N(d2) in Black Scholes Merton (FRM T4-12) - YouTube
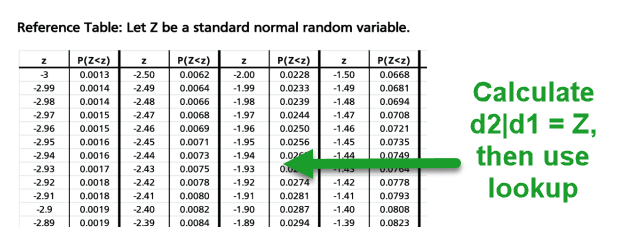
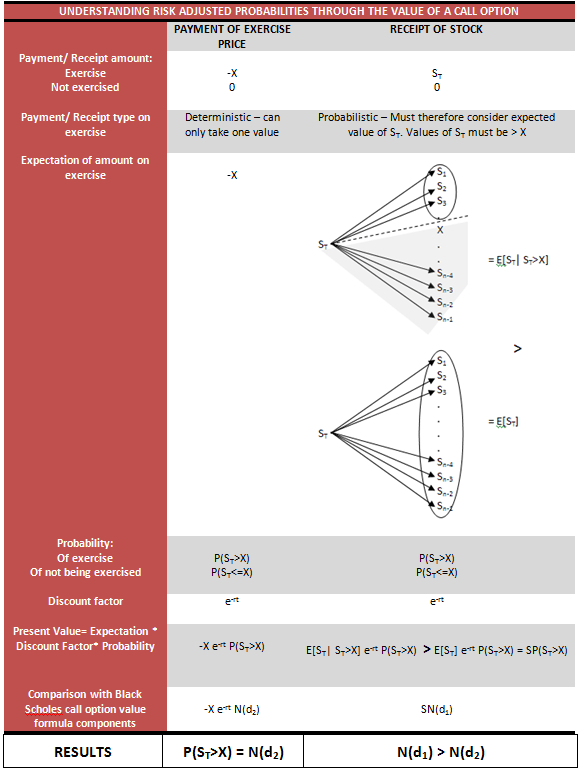
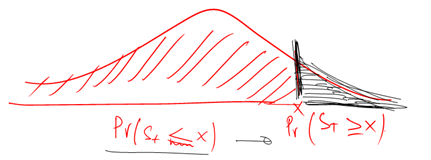
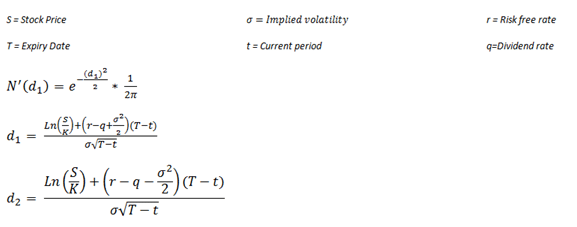Lecture 12: The Black-Scholes Model Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11
Understanding Alpha or Gamma Rent - FinanceTrainingCourse.com
Solved 9. Consider a financial market in which the | Chegg.com
Difference between N(d1) and N(d2) - FinanceTrainingCourse.com
Chapter 13. Black / Scholes Model - ppt download
stochastic calculus - Black-Scholes N(d1) and N(-d1) - Mathematics Stack Exchange
Black-Scholes-Merton | Brilliant Math & Science Wiki
SOLVED: Table 5.4 summarizes various BSM formulas and their Greeks: In(FIK) F = FA(0,t) = A(0)e^(-rt), d1,2 = (ln(F/A(0)) + (r + 0.5 * σ^2)t) / (σ√t) N(d) = (1/√(2π)) ∫e^(-x^2/2)dx from -
Help with Call option (ND1 Calculation) - The Student Room
Difference between N(d1) and N(d2) - FinanceTrainingCourse.com
How to interpret N(d1) and N(d2) in Black Scholes Merton (FRM T4-12) - YouTube
The Intuition Behind The Black Scholes Equation | by Moontower by Kris Abdelmessih | Medium
Reading negative d1 and d2 from Normal tables | Economics, Finance, Options | ShowMe
Consider a 1-year option with exercise price $60 on a stock with annual standard deviation 20%. The T-bill - brainly.com
Demystifying N(d1) and N(d2) in the Black Scholes Model - YouTube
How to interpret N(d1) and N(d2) in Black Scholes Merton (FRM T4-12) - YouTube
SOLVED: We denote by r > 0 the risk-free interest rate. Recall the Black-Scholes model and the Black-Scholes formula for a T-expiry; K-strike European call option written on S having positive constant
THE BLACK-SCHOLES-MERTON MODEL 指導老師：王詩韻老師 學生：曾雅琪 ( ) ，藍婉綺 ( ) - ppt download
SOLVED: Problem 1. Recall the Black-Scholes formula for the price of a European call option on a non-dividend paying stock is given by Ct = St × N (d1) - e-r(T-t) × K
In the black scholes formula how can N(d1) represent the expected return in the event of an exercise and at the same time also mean 'delta' - probability that the option will
Consider a 1-year option with exercise price $60 on a stock with annual standard deviation 20%. The T-bill rate is 3% per year. Find N(d1) for stock prices $55, $60, and $65. (
